A Response to “Is Numpy Faster than Python?”
So I woke up this morning to my google feed recommending the article Is NumPy Faster than Python? and the first thought through my head was “uhhh … why is that even a question?”. I later realized that this was a follow up to the author’s previous article called “Should You Jump Python’s Ship and Move to Julia?”.
Upon more investigation it was clear that the author (whose name is Emmett) is a Julia evangelist and he
seems very competent in Julia but based on the articles maybe relatively new to python.
Now this is … fine. I have a great deal of respect for Julia and the community around it and the
language has come a long way from when I first used it in grad school (as I noticed during my lengthy exploration
of the language in a past video).
In fact in the above video I did a comparison of how well a naive Julia implementation stacks up against a
naive Numba implementation of the same simulation (they were about the same). I was then schooled by some
folks much more knowledgable about Julia than I was after my 4 hours session with it and they demonstrated
that with a bit of care Julia could become sufficiently faster than Numba. The fact that such a simple looking
language could be made so performant says a lot about its potential and I’m eagerly looking forward to what
becomes of it.
But this post is not about Julia.
This post is more of a response to the “Is Numpy Faster than Python” question, but perhaps more importantly
it serves as an assertion that “Even if you wanted to, you likely cannot jump Python’s ship just yet, so
how about we talk about how to make the most of this unfortunately less than performant language?”
OK that’s a bit of a mouthful, sorry about that. Let’s get to it.
The base code⌗
What follows is code taken verbatim from the aforementioned article (formatting my own,
I just ran black on it). First, the pure Python implementation which was compared with Julia:
def dot(x, y):
lst = []
for i, w in zip(x, y):
lst.append(i * w)
return lst
def sq(x):
x = [c ** 2 for c in x]
return x
class LinearRegression:
def __init__(self, x, y):
# a = ((∑y)(∑x^2)-(∑x)(∑xy)) / (n(∑x^2) - (∑x)^2)
# b = (x(∑xy) - (∑x)(∑y)) / n(∑x^2) - (∑x)^2
if len(x) != len(y):
pass
# Get our Summations:
Σx = sum(x)
Σy = sum(y)
# dot x and y
xy = dot(x, y)
# ∑dot x and y
Σxy = sum(xy)
# dotsquare x
x2 = sq(x)
# ∑ dotsquare x
Σx2 = sum(x2)
# n = sample size
n = len(x)
# Calculate a
self.a = (((Σy) * (Σx2)) - ((Σx * (Σxy)))) / ((n * (Σx2)) - (Σx ** 2))
# Calculate b
self.b = ((n * (Σxy)) - (Σx * Σy)) / ((n * (Σx2)) - (Σx ** 2))
def predict(self, xt):
xt = [self.a + (self.b * i) for i in xt]
return xt
The code is meant to do Linear Regression and the API is kind of similar to what you might expect
from scikit-learn (except the initializer takes the place of the fit function). If I came across this code
in a review I would make the following remarks:
- The “if not this then pass” in the initializer is problematic. Kindly replace with an assert or, if you’d prefer not to raise an exception, then let’s talk more about your usecase and how you might redesign this.
- Use
Numpyarrays and ops rather thanPythonlists and ops. - There is already an implementation of this in
scikit-learn, is there any reason why you can’t use that (e.g. don’t want to pull in a dependency)?
Now Emmett did rewrite the code with Numpy (again, formatting my own and I have removed the comments):
import numpy as np
class npLinearRegression:
def __init__(self, x, y):
if len(x) != len(y):
pass
Σx = sum(x)
Σy = sum(y)
xy = np.multiply(x, y)
Σxy = sum(xy)
x2 = np.square(x)
Σx2 = sum(x2)
n = len(x)
self.a = (((Σy) * (Σx2)) - ((Σx * (Σxy)))) / ((n * (Σx2)) - (Σx ** 2))
self.b = ((n * (Σxy)) - (Σx * Σy)) / ((n * (Σx2)) - (Σx ** 2))
def predict(self, xt):
xt = [self.a + (self.b * i) for i in xt]
return xt
but it’s a bit of an unfortunate implementation (and only gives about a 50% speedup over pure Python and is 5x or so slower than Julia). Let’s
pretend this is the update to the previous code that was submitted after my pretend review of the above code.
My next review would likely be as follows:
- You appear to ultimately still be operating over
=Python=lists and there’s probably a lot of casting back and forth betweenndarrayandList. np.multiplyandnp.squarearen’t really needed (ifxandyare passed asnumpyarrays, that is).- The
predictfunction is completely unchanged.
At this point I might offer the reviewee to do some pair programming with me so I can demonstrate some of the updates this code can dearly benefit from. At the end of that review the code would likely look something like this:
import numpy as np
class NpLinearRegression:
def __init__(self, x: np.ndarray, y: np.ndarray) -> None:
assert len(x) == len(y), "x and y arrays must have the same number of elements along the first axis"
Σx = x.sum()
Σy = y.sum()
Σxy = (x*y).sum()
Σx2 = (x**2).sum()
n = len(x)
self.a = (((Σy) * (Σx2)) - ((Σx * (Σxy)))) / ((n * (Σx2)) - (Σx ** 2))
self.b = ((n * (Σxy)) - (Σx * Σy)) / ((n * (Σx2)) - (Σx ** 2))
def predict(self, xt: np.ndarray) -> np.ndarray:
return self.a + (self.b * xt)
At first blush this may look exactly the same as the last numpy implementation but it’s subtly different.
All arrays are now np.ndarray (as made clear to the reader and any linters/static checkers by the type hints).
This not only makes the code smaller ([self.a + self.b*i for i in xt] vs self.a + self.b*xt but also makes it
much faster since all iterations over the arrays now happen in c rather than pure python.
The Tests⌗
I’m too lazy to grab the original post’s source data so I’m just going to generate my own. Here’s my testbed:
import time
import numpy as np
factory_map = {'pure_python': LinearRegression,
'numpy_orig': npLinearRegression,
'numpy_correct': NpLinearRegression}
times_by_method = {}
Ns = [1000, 10000, 100000, 1000000, 10000000]
for method, factory in factory_map.items():
print(method)
times = []
for N in Ns:
print(N)
x = np.linspace(0, 1, N)
y = x + np.random.rand(N)*0.1
start = time.time()
for i in range(10):
_ = factory(x, y).predict(x)
times.append(time.time() - start)
times_by_method[method] = times
Pretty simple, for each implementation I’m generating data of length 1000 all the way to 10 million (which was
the number used for the original implementation). Note that the difference between the original two codes
and a correct numpy implementation is so staggering that I have to put it on a log plot…
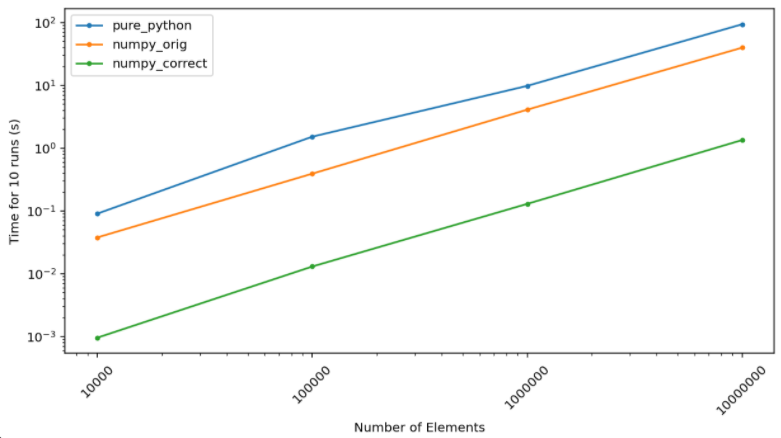
The absolute numbers here don’t quite matter (and don’t quite mean anything) and can’t be directly compared
with the Emmett’s Julia implementation since the machine these ran on (in this case a Google colab notebook)
is not the same as the one used for previous tests. Nevertheless we can compare speedups.
For the 10,000,000 elements case, 10 total runs take 93 seconds in pure python. With the original numpy
implementation this goes down to about 39 seconds which is consistent with Emmett’s testing. A correct numpy
implementation, however, gets you to a mere 1.3 seconds… that’s a roughly 72x speedup.
I unfortunately cannot also compare this to Emmett’s python vs Julia comparison by comparing the speedups
since the timing is not apples to apples. I can still try though it’s not clear if the Julia @time magic he ran was the first
run of the session or not (since that may or may not involve the JIT compiler) and how many runs of the function
it did. It might have been a single run in which case the Python timing would be 1.22 seconds, implying
Julia’s speed up to be only about 4x. Having used Julia before I’m reasonably certain that’s wrong.
So what’s the takeaway here?⌗
- We’re likely stuck with
Pythonwhen it comes to ML and data science (this is an assertion more so than a conclusion). - We should learn to use the various tools at our disposal correctly, and learning to grok
numpygoes a long way. - When comparing the performance of two systems it’s a good idea to make sure you understand at least some intricacies of both.
When I started writing this I thought it may make sense to do a comparison with Numba as well, but this post is already gotten
too long and I have to start my work day so I’ll end it here. I would also like to invite Emmett to update his
article to include my numpy implementation.
Cheers!